More recursion examples

The real advantages of recursion become evident when we come across problems where iterative solutions are difficult to write. Let's take a look at binary trees, for instance. A binary tree is a branched structure where we have nodes, and at each node the structure branches, at most, into two child branches with nodes of their own. A binary tree could then look like this (computer science is often considered a branch of the natural sciences, but our understanding of trees is a little topsy-turvy, as you'll notice):

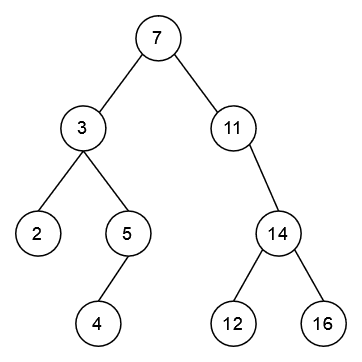
Binary trees should at least theoretically be easy to handle recursively: if we want to perform some operation on every node in the tree, our algorithm simply needs to

1. Process the current node
2. Call itself on the child node on the left
3. Call itself on the child node on the right

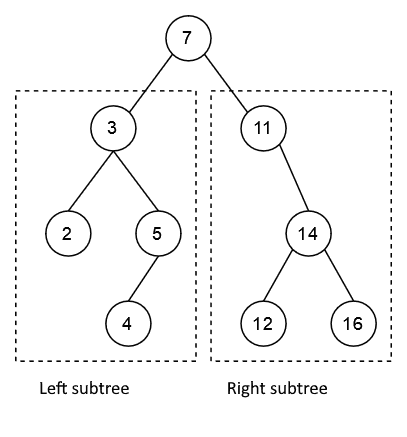
As you can see from the image above, both the left and right "subtrees" are fully fledged binary trees themselves, and the only node left outside the recursive calls is the parent node, which is processed in step 1, before calling the function recursively. So, we can be sure that when the execution of the function finishes, each node has been visited exactly once.

An iterative version of a binary tree traversal would be much more complicated, as we would have to somehow keep track of all the nodes we have already visited. The same principles are true for all computational tree structures, not just binary ones.

A binary tree is easily modelled in Python code as well. We only need to write a class definition for a single node. It has a value attribute and attributes for the left and right child nodes:

class Node:
    """ The class represents a single node in a binary tree """
    def __init__(self, value, left_child:'Node' = None, right_child:'Node' = None):
        self.value = value
        self.left_child = left_child
        self.right_child = right_child

Now let's assume we want to model the following tree:

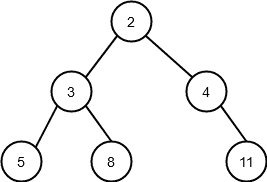
We could achieve this with the following code:

if __name__ == "__main__":
    tree = Node(2)

    tree.left_child = Node(3)
    tree.left_child.left_child = Node(5)
    tree.left_child.right_child = Node(8)

    tree.right_child = Node(4)
    tree.right_child.right_child = Node(11)

Recursive binary tree algorithms

First, let's take a look at an algorithm which prints out all the nodes in a binary tree one by one. In these following examples we will be working with the binary tree defined above.

The argument to the printing function is the root node of the binary tree. This is the node at the very top in our illustration above. All other nodes are children to this node:

def print_nodes(root: Node):
    print(root.value)

    if root.left_child is not None:
        print_nodes(root.left_child)

    if root.right_child is not None:
        print_nodes(root.right_child)

The function prints the value of the node passed as an argument, and then calls itself on the left and right child nodes, assuming the nodes are defined. This is a very simple algorithm, but it efficiently and reliably traverses all nodes in the tree, no matter the size of the tree. Crucially, no node is visited twice. Each value is printed only once.

If we pass the root node tree of the binary tree illustrated above as an argument to the function, it prints out

As you can see from the order of the nodesin the printout, the algorithm first moves down the "left leg" of the tree down to the very bottom, and from there traverses the other nodes in order.

Similarly, we can write an algorithm for calculating the sum of all the values stored in the nodes of the tree:

def sum_of_nodes(root: Node):
    node_sum = root.value

    if root.left_child is not None:
        node_sum += sum_of_nodes(root.left_child)

    if root.right_child is not None:
        node_sum += sum_of_nodes(root.right_child)

    return node_sum

The variable node_sum is initialised to equal the value of the current node. The value in the variable is then augmented by recursive calls to the node sums of the left and right child trees (first making sure they exist, of course). This result is then returned

A sorted binary tree

A binary tree is especially useful when the nodes are sorted in a certain way. This makes finding nodes in the tree fast and efficient.

Let's take a look a tree which is sorted as follows: the left child of each node is smaller than the node itself, and the right child is correspondingly greater.

Now we can write a recursive algorithm for searching for nodes. The idea is very similar to the binary search from the previous section: if the current node is the node we are looking for, return True. Else, continue recursively with either the left or the right child tree. If the node is not defined, return False.

def find_node(root: Node, value):
    if root is None:
        return False

    if value == root.value:
        return True

    if value > root.value:
        return find_node(root.right_child, value)

    return find_node(root.left_child, value)

Revisiting the times before recursion

Let's finish off this part of the material with a slightly larger exercise concentrating on object oriented programming principles. We do not recommend using recursion in this series of tasks, but list comprehension techniques will come in useful.

Please respond to a quick questionnaire on this part of the course.

You can check your current points from the blue blob in the bottom-right corner of the page.